The Lottery Ticket Hypothesis: A Survey
Published:
Metaphors are powerful tools to transfer ideas from one mind to another. Alan Kay introduced the alternative meaning of the term ‘desktop’ at Xerox PARC in 1970. Nowadays everyone - for a glimpse of a second - has to wonder what is actually meant when referring to a desktop. Recently, Deep Learning had the pleasure to welcome a new powerful metaphor: The Lottery Ticket Hypothesis (LTH). But what idea does the Hypothesis try to transmit? In todays post we dive deeper into the hypothesis and review the literature after the original ICLR best paper award by Frankle & Carbin (2019).
Table of Contents
- Pruning in Deep Learning

- The Lottery Ticket Hypothesis & How to Scale it

- Dissecting Lottery Tickets: Robustness & Learning Dynamics

- Detecting Winning Tickets with Little to No Training

- Do Tickets Generalize across Datasets, Optimizers and Domains?



- Open Research Questions

- References

Pruning in Deep Learning 
Pruning over-parametrized neural networks has a long tradition in Deep Learning. Most commonly it refers to setting a particular weight to 0 and freezing it for the course of any subsequent training. This can easily be done by element-wise multiplying the weights $W$ with a binary pruning mask $m$. There are several motivating factors for performing such a surgical intervention:
- It supports generalization by regularizing overparametrized functions.
- It reduces the memory constraints during inference time by identifying well-performing smaller networks which can fit in memory.
- It reduces energy costs, computations, storage and latency which can all support deployment on mobile devices.
With the recent advent of deeper and deeper networks all 3 factors have been seeing a resurgence in attention. Broadly speaking any competitive pruning algorithm has to address 4 fundamental questions:
-
What connectivity structures to prune?: Unstructured pruning does not consider any relationships between the pruned weights. Structured pruning, on the other hand, prunes weights in groups, e.g. by removing entire neurons (weight columns), filters or channels of CNNs. Although unstructured pruning often allows to cut down the number of weights more drastically (while maintaining high performance), this does not have to speed up computations on standard hardware. The key here is that dense computations can easily be parallelized while ‘scattered’ computations can’t. Another distinction has to be made between global and local pruning. Local pruning enforces that one prunes $s$ percent of weights from each layer. Global pruning, on the other hand, is unrestricted and simply requires that the total number of weights across the entire network is pruned by $s$ percent.
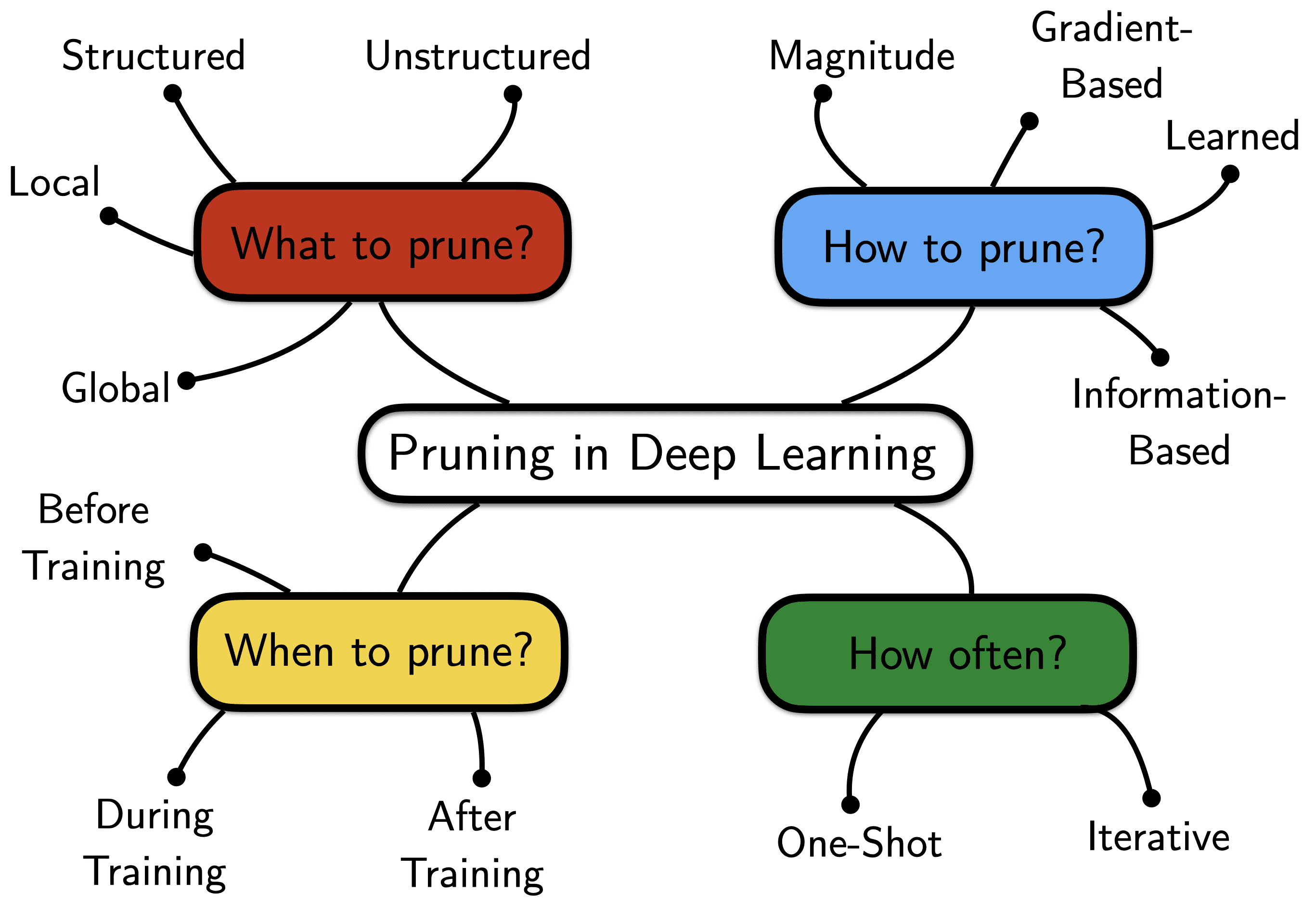
Fig. 1: What, How, When and How often to prune?
-
How to rank weights to prune?: There are many more or less heuristic ways to score the importance of a particular weight in a network. A common rule of thumb is that large magnitude weights have more impact on the function fit and should be pruned less. While working well in practice, this intuitively may seem to contradict ideas such as $L_2$-weight regularization which actually punishes large magnitude weights. This motivates more involved techniques which learn pruning masks using gradient-based methods or even higher-order curvature information.
-
How often to prune?: Weight magnitude is often only a noisy proxy for weight importance. Pruning only a single time at the end of training (one-shot) can become victim to this noise. Iterative procedures, on the other hand, prune only a small number of weights after one training run but reiterate the train - score - prune - rewind cycle. This often times helps to de-noise the overall pruning process. Commonly the pruning rate per iteration is around 20% and a total of 20 to 30 pruning iterations are used (which leaves us with only 1% percent of non-pruned weights). One can be more conservative - at the cost of training for a lot longer!
- When to perform the pruning step?: One can perform pruning at 3 different stages of network training - after, during and before training. When pruning after the training has converged the performance often decreases, which makes it necessary to retrain/fine-tune and to give the network a chance to readjust. Pruning during training, on the other hand, is often associated with regularization and ideas of dropout/reinforcing distributed representations. Until very recently it was impossible to trained sparse networks from scratch.
The Lottery Ticket Hypothesis & How to Scale it 
Frankle & Carbin (2019) - The Lottery Ticket Hypothesis: Finding Sparse, Trainable Neural Networks
Paper | Code
While the traditional literature has been able to show that a fully trained dense network can be pruned to little parameters without degrading performance too much, for a long time it has been impossible to successfully train a sparse sub-network from scratch. So why might this the case? The smaller subnetwork can approximate a well performing function. But the learning dynamics appear to be very different compared to the dense network.
The original lottery ticket hypothesis paper (Frankle & Carbin, 2019) first provided insight why this might be the case: After pruning the resulting sub-networks were randomly initialized. If one instead re-initializes the weights back to their original (but now masked) weights $m \odot W_0$, it is possible to recover performance on par (or even better!) in potentially fewer training iterations. These high-performing sub-networks can then be thought of as winners of the weight initialization lottery. The hypothesis goes as follows:
The Lottery Ticket Hypothesis: A randomly-initialized, dense neural network contains a subnetwork that is initialised such that — when trained in isolation — it can match the test accuracy of the original network after training for at most the same number of iterations. - Frankle & Carbin (2019, p.2)
So how can we attempt to find such a winning ticket? Frankle & Carbin (2019) propose iterative magnitude pruning (IMP): Starting from a dense initialization $W_0$ we train our network until convergence to obtain $W_{T^\star}^{(1)}$. Afterwards, we determine the $s$ percent smallest magnitude weights and create a binary mask $m^{(1)}$ that prunes these. We then retrain the sparsified network with its previous initial weights $m^{(1)} \odot W_0$. After convergence we repeat the pruning process (masking additional $s^2$ weights) and reset to the initial weights with the newly found mask $m^{(2)}$. We iterate this process until we reach the desired level of sparsity or the test accuracy drops significantly.
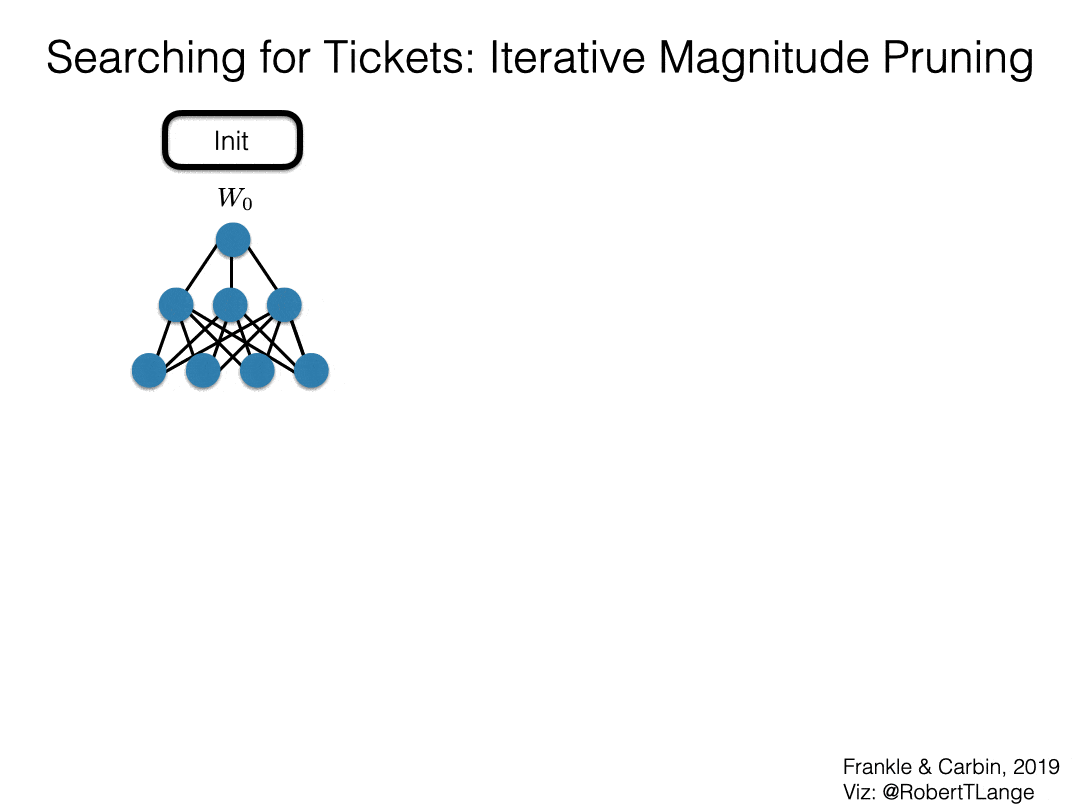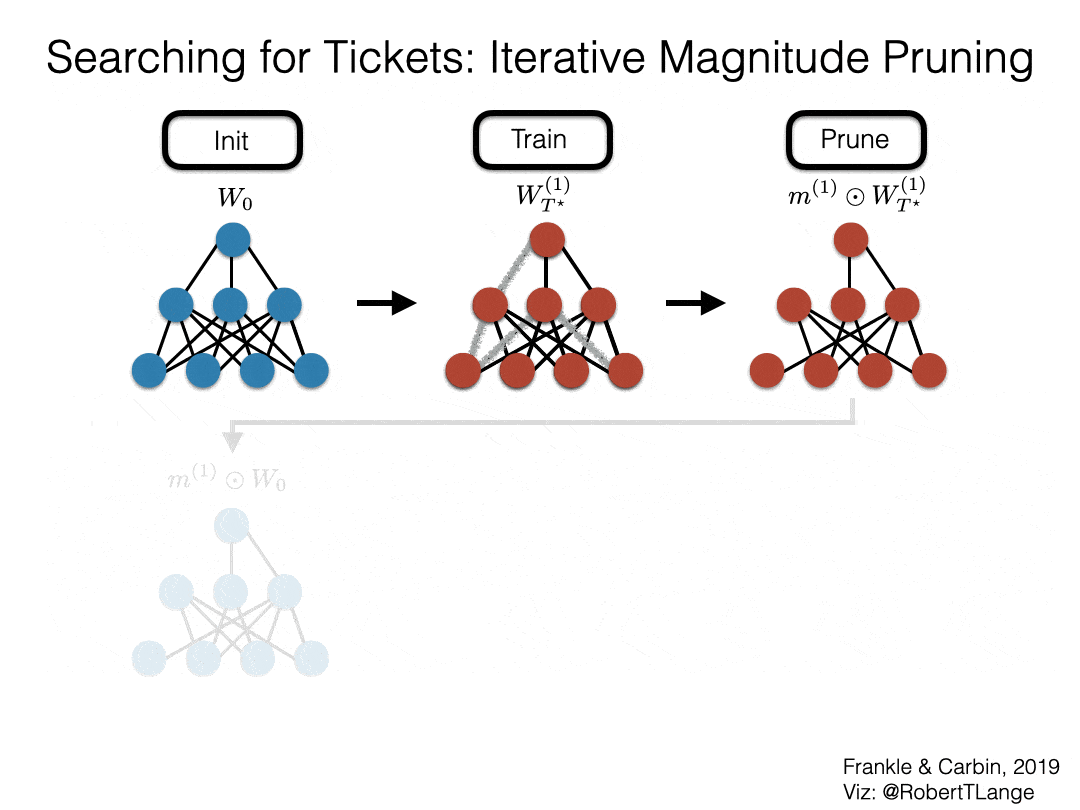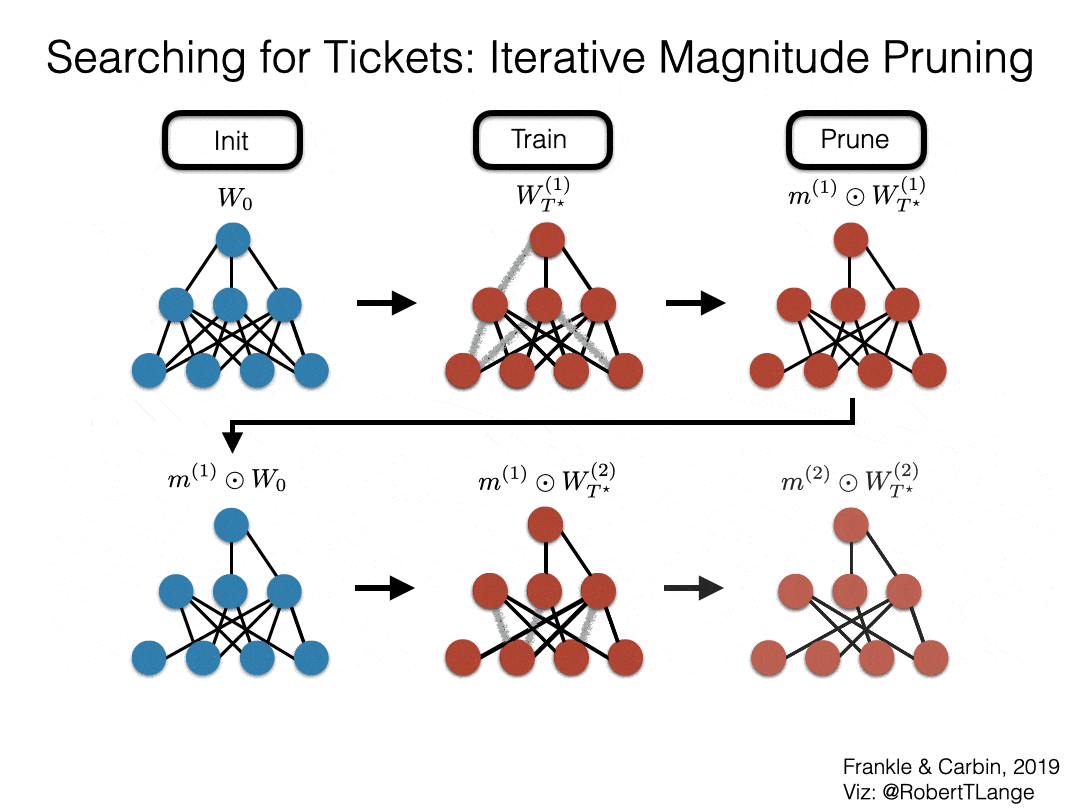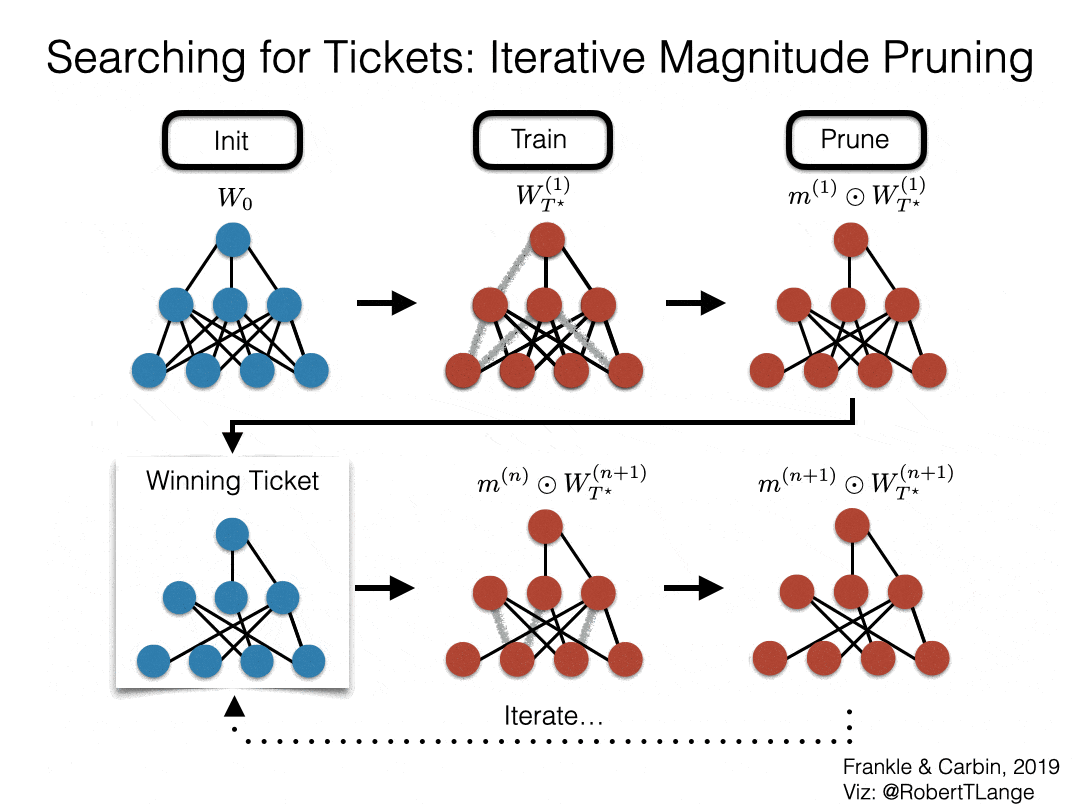
Fig. 2: Lottery Ticket Hypothesis - IMP procedure (Frankle & Carbin, 2019)
If IMP succeeds it finds the winner of the initialization lottery. This is simply the subnetwork $m^{(n)} \odot W_0$ that remains after this iterative pruning process. Note that it is also possible to simply prune in a one-shot fashion - but better results are obtained when spending that extra compute (see figure 4 of Frankle & Carbin (2019)). If we think back to the broad questions of the pruning literature IMP fits in as follows:
Fig. 3: IMP and the pillars of pruning
Some key empirical insights of the very first LTH paper are summarized in the figure below:
- Panel A: Randomly reinitializing & re-training pruned networks leads to deteriorated performance. Results shown are on MNIST with the LeNet architecture.
Fig. 4: LTH key results. Source: Adapted from Frankle & Carbin (2019)
-
Panel B: Without any hyperparameter adjustments IMP is able to find sparse subnetworks that are able to outperform un-pruned dense networks in fewer training iterations (the legend refers to the percentage of pruned weights). The gap in final performance between a lottery winning initialization and a random re-initialization is referred to as the lottery ticket effect.
-
Panel C & Panel D: In order to scale the original results to more complicated tasks/architectures like CIFAR-10, VGG-19 and Resnet-20, Frankle & Carbin (2019) had to adapt the learning rate as well as include a warmup (annealing from 0 to the final rate within a predefined set of iterations) schedule. Note that the required Resnet learning rate is a lot smaller than the VGG-19 learning rate.
So what can this tell us? First, IMP can find a substructure that is favourable for the task at hand and that the weight initialization of that subnetwork is special in terms of learning dynamics. Furthermore, over-parametrization is not necessary for successful training - it may only help by providing a combinatorial explosion of available subnetworks. A lot of the interesting follow-up work characterizes potential mechanisms behind the qualitative differences of winning tickets.
Frankle, Dziugaite, Roy, & Carbin (2019) - Stabilizing the Lottery Ticket Hypothesis
Paper | Code
One limitation of the original lottery ticket paper was that its restriction to small-scale tasks such as MNIST and CIFAR-10. In order to scale the LTH to competitive CIFAR-10 architectures, Frankle & Carbin (2019) had to tune learning rate schedules. Without this adjustment it is not possible to obtain a pruned network that is on par with the original dense network (Liu, Sun, Zhou, Huang, & Darrell, 2018; Gale, Elsen, & Hooker, 2019). But what if we loosen up some of the ticket restrictions?
In follow-up work Frankle, Dziugaite, Roy, & Carbin (2019) asked whether it might be possible to robustly obtain pruned subnetworks by not resetting the weights to their initial values $W_0$ but to weights found after a small number of $k$ training iterations. In other words, instead of rewinding to iteration 0 after pruning, we rewind to iteration $k$. Here is the formal definition and a graphical illustration:
The Lottery Ticket Hypothesis with Rewinding: Consider a dense, randomly-initialized neural network $f(x;W_0)$ that trains to accuracy $a^\star$ in $T^\star$ iterations. Let $W_t$ be the weights at iteration $t$ of training. There exist an iteration $k « T^\star$ and fixed pruning mask $m \in \{0, 1\}^{\mid W_0 \mid}$ (where $\mid\mid m\mid\mid_1 « \mid W_0 \mid $) such that subnetwork $m \odot W_k$ trains to accuracy $a \geq a^\star$ in $T \leq T^\star - k$ iterations. - Frankle et al. (2019, p. 2)

Fig. 5: 'Matching Ticket' Hypothesis - IMP with Rewinding (Frankle et al., 2019)
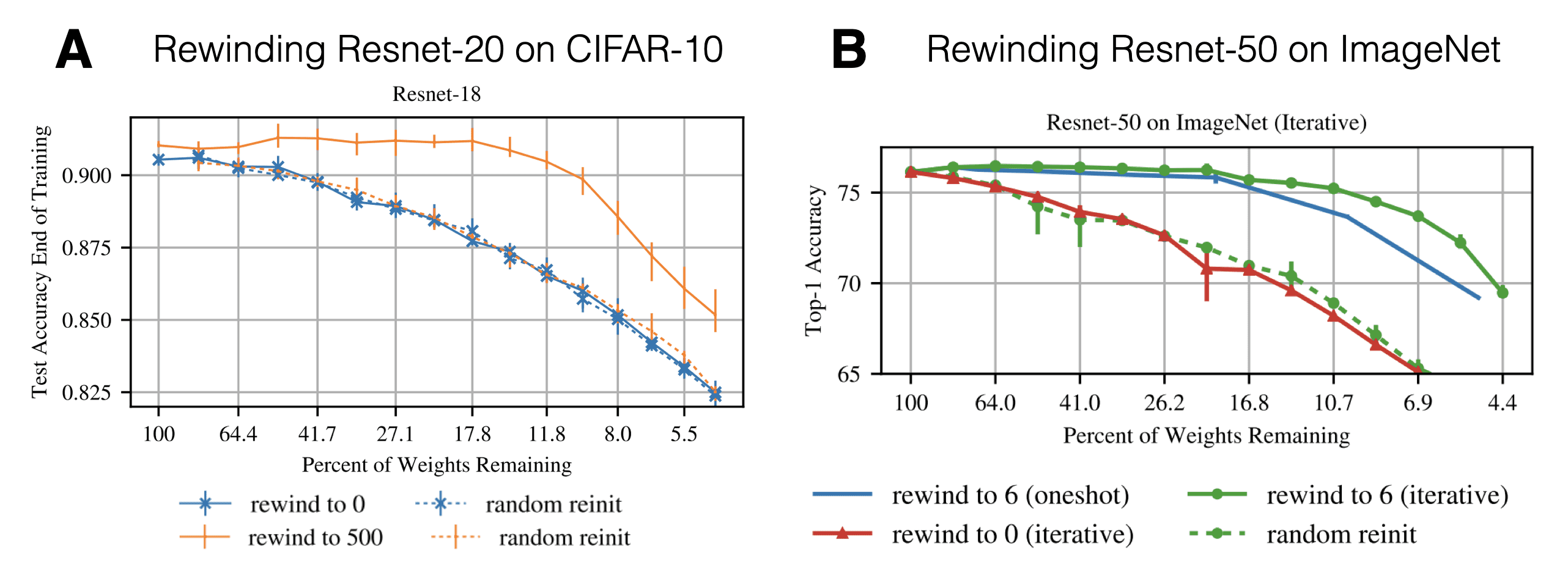
Since we perform a little bit of training, the resulting ticket $m^{(n)}, W^{(k)}$ is no longer called a lottery ticket but a matching ticket. The key insights are summarized in the figure below: Rewinding to an iteration $k > 0$ is highly effective when performing IMP. It is possible to prune up to ca. 85% of the weights while still obtaining matching test performance. This holds for both CIFAR-10 and Resnet-20 (rewinding to iteration 500; panel A) as well as ImageNet and Resnet-50 (rewind to epoch 6; panel B). There is no longer a need for a learning rate warmup.
Fig. 6: Scaling the LTH key results. Source: Adapted from Frankle et al. (2019)
Renda, Frankle, & Carbin (2020) - Comparing Rewinding and Fine-tuning in Neural Network Pruning
Paper | Code
Until now we have discussed whether IMP is able to identify a matching network initialization. But how does the lottery procedure compare to other pruning methods? In their paper, Renda, Frankle, & Carbin (2020) compare between three different procedures:
- Fine-Tuning: After pruning, the remaining weights are trained from their final trained values using a small learning rate. Usually this is simply the final learning rate of the original training procedure.
- Weight Rewinding: This corresponds to the previously introduced method by Frankle et al. (2019). After pruning, the remaining weights are reset to the value of a previous SGD iteration $k$. From that point on the weights are retrained using the learning rate schedule from iteration $k$ onwards. Both weights and learning rate schedule are reset.
- Learning Rate Rewinding: Instead of rewinding the weight values and setting back the learning rate schedule, learning rate rewinding uses the final unpruned weight and only resets the learning rate schedule to iteration $k$.
Renda et al. (2020) contrast gains and losses of the three methods in terms of accuracy, search cost and parameter-efficiency. They answer the following questions:
-
Given an unlimited budget to spend on search cost, how do final accuracy and parameter efficiency (compression ratio pre/post pruning) behave for the 3 methods?
-
Given a fixed budget to spend on search cost, how do all 3 methods compare in terms of accuracy and parameter efficiency?
Experiments on Resnet-34/50/56 and the natural language benchmark GNMT reveal the following insights:
- Weight rewinding and retraining outperforms simple fine-tuning and retraining in both unlimited and fixed budget experiments. The same holds when comparing structured and unstructured pruning.
- Learning rate rewinding outperforms weight rewinding. Furthermore, while weight rewinding can fail for $k=0$, it is almost always beneficial to rewind the learning rate to the beginning of the training procedure.
- Weight rewinding LTH networks is the SOTA method for pruning at initialisation in terms of accuracy, compression and search cost efficiency.
As with many empirical insights into Deep Learning which are generated by large-scale experiments there remains one daunting question: What does this actually tell us about these highly non-linear systems we are trying to understand?
Dissecting Lottery Tickets: Robustness & Learning Dynamics 
Zhou, Lan, Liu, & Yosinski (2019) - Deconstructing lottery tickets: Zeros, signs, and the supermask
Paper | Code
What are the main ingredients that determine whether an initialization is a winning ticket or not? It appears to be the combination of the masking criterion (magnitude of the weights), the rewinding of the non-masked weights, and the masking that sets weights to zero and freezes them. But what if we change any one of these 3 ingredients? What is special about large weights? Do other alternative rewinding strategies preserve winning tickets? And why set weights to zero? Zhou, Lan, Liu, & Yosinski (2019) investigate these questions in 3 ways:
- By comparing different scoring measures to select which weights to mask. Keeping the smallest trained weights, keeping the largest/smallest weights at initialisation, or the magnitude change/movement in weight space.
- By analyzing if one still obtains winning tickets when rewinding weights not to their original initialization. They compare random reinitialisation, reshuffling of kept weights and a constant initialisation.
- By freezing masked weights not to the value of 0 but to their initialisation value.
The conclusions of extensive experiments are the following:
- Other scoring criteria that maintain weights “alive” proportionately to their distance from the origin perform equally well as the ‘largest magnitude’ criterion.
- As long as one keeps the same sign as the original sign of the weights at initialisation when performing rewinding, one can obtain lottery tickets that perform on par with the classical IMP formulation (Note: This finding could later not be replicated by Frankle et al. (2020b)).
- Masking weights to the value 0 is crucial.
Based on these findings they postulate that ‘informed’ masking can be viewed as a form of training: It simply accelerates the trajectory of weights which were already “heading” to zero during their optimization trajectory. Interestingly, a mask obtained from IMP applied to a randomly initialized network already (and without any additional training) yields performance that vastly outperforms a random mask and/or randomly initialized network. Hence, it is a form of supermask that encodes a strong inductive bias. This opens up an exciting perspective of not training network weights at all and instead simply finding the right mask. Zhou et al. (2019) show that it is even possible to learn the mask by making it differentiable and training it with a REINFORCE-style loss. This idea very much reminds me of Gaier & Ha’s (2019) Weight Agnostic Neural Networks. A learned mask can be thought of as a connectivity pattern that encodes a solution regularity. By sampling weights multiple times to evaluate a mask, we essentially make it robust (or agnostic) to the sampled weights.
Frankle, Dziugaite, Roy, & Carbin (2020a) - Linear Mode Connectivity & the Lottery Ticket Hypothesis
Paper | Code
When we train a neural network, we usually do so on a random ordering of data batches. Each batch is used to evaluate a gradient of the loss with respect to the network parameters. After a full loop over the dataset (aka an epoch) the batches are usually shuffled and we continue with the next epoch. The sequence of batches can be viewed as a source of noise which we inject into the training procedure. Depending on it, we might obtain very different final weights, but ideally our network training procedure is somewhat robust to such noise. More formally, we can think of single weight initialization $W_0$ which we train on two different batch orders to obtain the trained weights $W_T^1$ and $W_T^2$. Linear mode connectivity analysis (Frankle, Dziugaite, Roy, & Carbin, 2020a) asks the following question: How does the validation/test accuracy behave if we smoothly interpolate (convex combination) between these two final weight configurations resulting from the different data orders?
Fig. 7: Linear Mode Connectivity. Source: Frankle et al. (2020a)
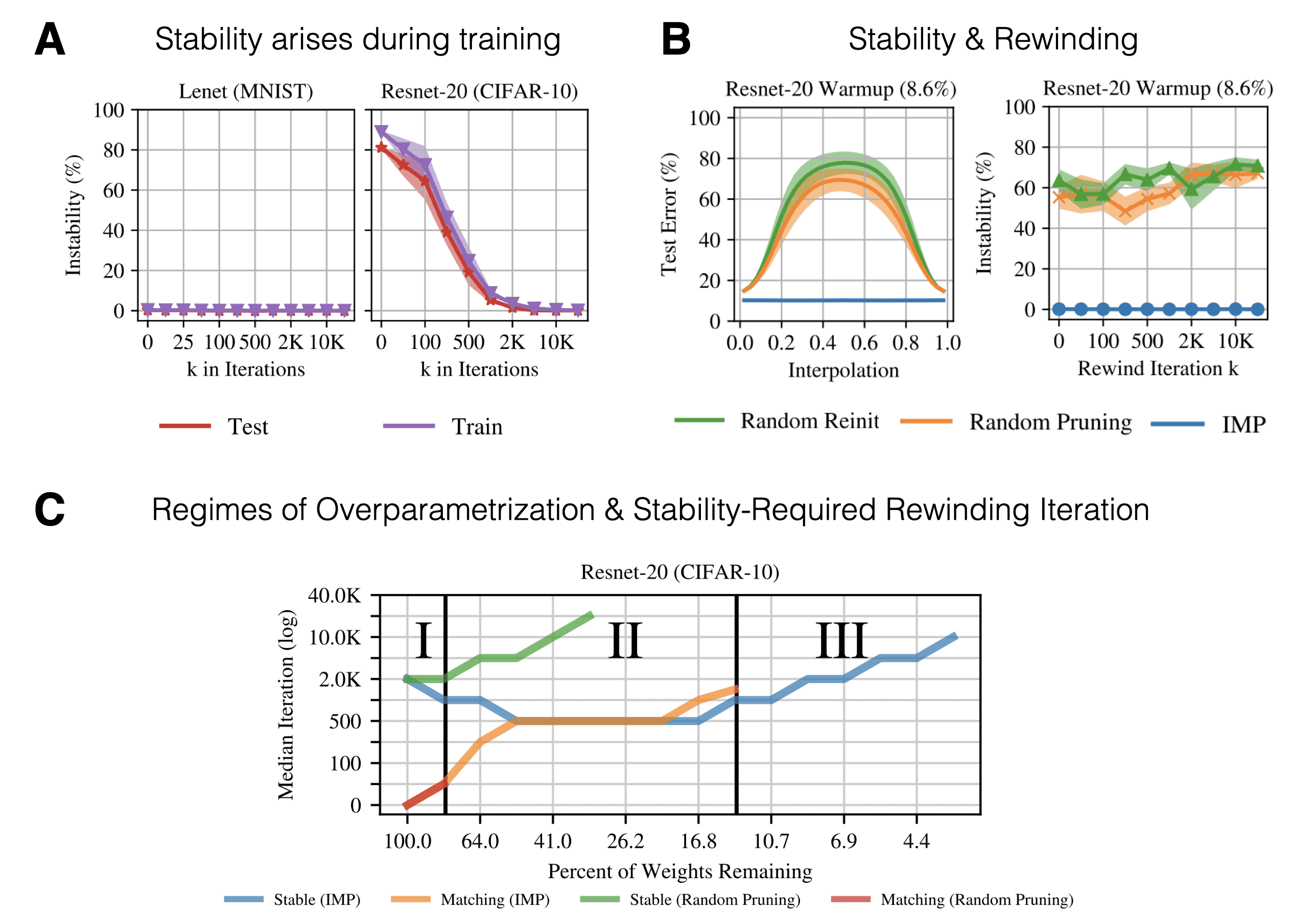
A network is referred to as stable if the error does not increase significantly as we interpolate between the two final weights. Furthermore, we can train $W_0$ to $W_k$ on a single shared data ordering and only later split the training into two separate data orders. For which $k$ does the network then become stable? Trivially, this is the case for $k=T$, but what about earlier ones? As it turns out this is related to the iteration to which we have to rewind in order to obtain a matching ticket initialisation.
Fig. 8: Linear Mode Connectivity key results. Source: Adapted from Frankle et al. (2020a)
-
Panel A: No tickets for now, just take a look at when the network becomes interpolation-stable to different data orderings. For LeNet this is already the case at initialization. For Resnet-20 this stability arises only later on in training. Isn’t this reminiscent of the rewinding iteration?
-
Panel B: Iterative magnitude pruning can induce stability. But this only works in combination with the learning rate schedule trick when rewinding to $k=0$.
-
Panel C: There appear to be 3 regimes of parametrization which we move into by pruning more and more weights (focus on the blue line):
- Regime I: The network is strongly overparametrized so that even random pruning still results in good performance.
- Regime II: As we increase the percentage of pruned weights only IMP yields matching and stable tickets/networks.
- Regime III: While IMP is still able to yield stable networks at severe sparsity, the resulting networks are no longer matching.
This is an example of how lottery tickets have been used to reveal characteristics of learning dynamics. Another more fine-grained analysis of different learning phases is given by the next paper:
Frankle, Schwab, & Morcos (2020) - The Early Phase of Neural Network Training
Paper | Code
So far we have seen that only a few training iterations (or epochs on Resnet) result in data-order robustness as well as the ability to obtain matching tickets when rewinding. A more general follow-up question is: How robust are these matching ticket initializations? How much can we wiggle and perturb the initialization before we loose the magical power? And how does this change with $k$?
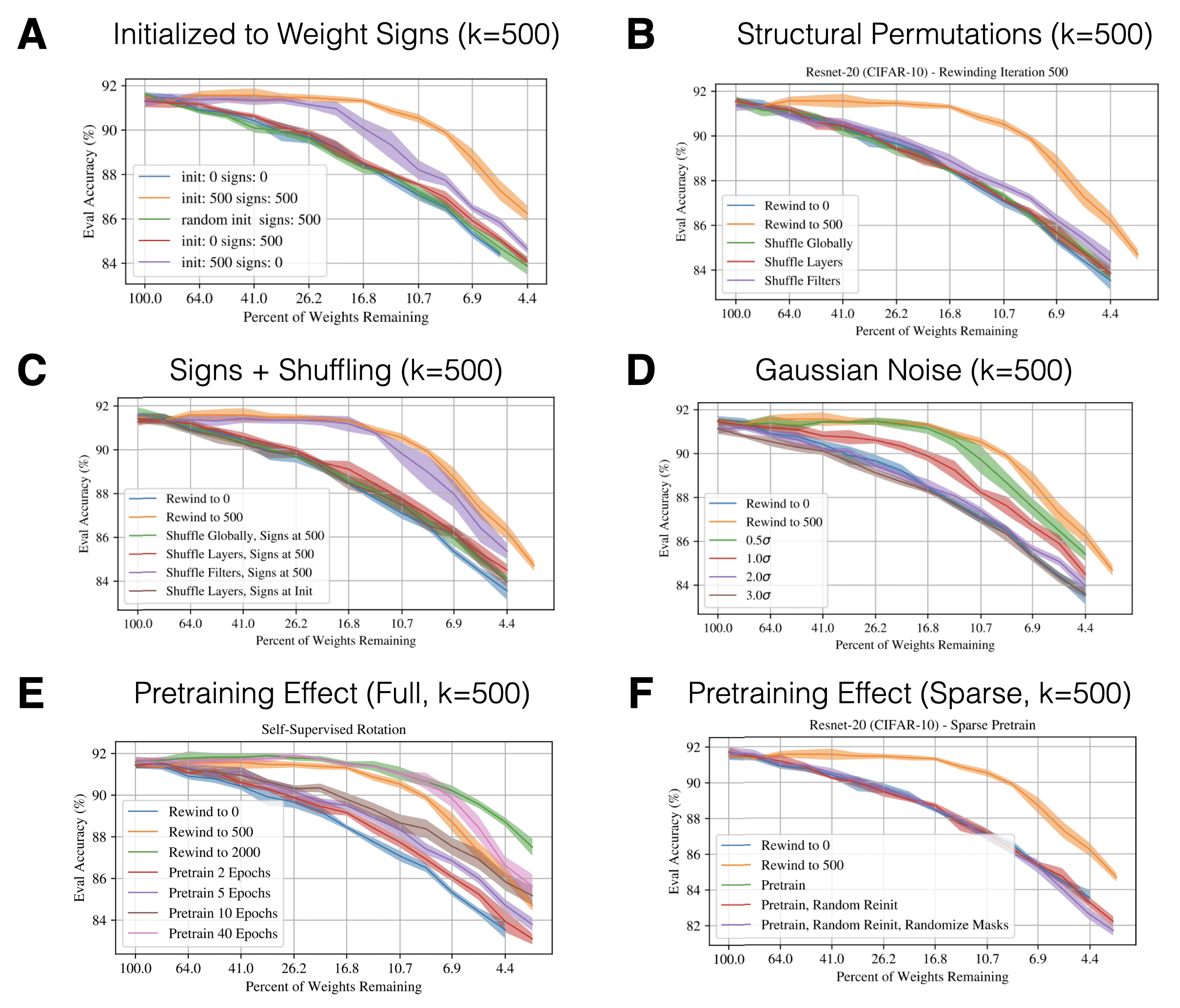
In order to study the emergence of robustness Frankle et al. (2020b) performed permutation experiments using Resnet-20 on CIFAR-10. The protocol goes as follows: Derive a matching ticket using IMP with rewinding. Afterwards, perform a perturbation to the matching ticket and train until convergence. The permutations include:
- Setting the weights to the signs and/or magnitudes of iteration 0 or $k$ (see panel A). Any permutation (sign or magnitude - ‘init’) hurts performance at high levels of sparsity. At low levels, on the other hand, the IMP-derived network appears to be robust to sign-flips. The same qualitative result holds for rewinding to $k=2000$ (see figure 4 of Frankle et al. (2020b)).
- Permute the weights at iteration $k$ with structural sub-components of the net (see panel B). This includes exchanging weights of the network globally (across layers), locally (within a layer) and within a given filter. The matching ticket is not robust to any of the perturbations and performance decreases to the level of rewinding to iteration $k=0$ . Panel C, on the other hand, limits the effect of permutation by only exchanging weights which have the same sign. In this case the network is robust to within filter shuffles at all sparsity levels.
- Add Gaussian noise to the matching ticket weights (see panel D): In order to assure the right scale of the added noise, Frankle et al. (2020b) calculate a layer-wise normalized standard deviation $\sigma$ resulting from initialization distribution of the specific layer. The size of the effective standard deviation very much affects the final performance of the perturbed lottery ticket. Larger perturbations = worse performance.
- Pretraining of a dense/sparse network with different self-supervised losses (panel E): The previous results are largely preserved when going from $k=500$ to $k=2000$. This is indicative that there are other forces than simply weight distribution properties and signs. Instead it appears that the magic lies in the actual training. Hence, Frankle et al. (2020b) asked whether the early phase adaptations depend on information in the conditional label distribution or whether unsupervised representation learning is sufficient. Training for a small number of epochs on random labels does close the gap compared to rewinding to iteration 0. But longer pre-training can eventually hurt the performance of the network. Finally, pre-training (non-ticket) sparse networks is not sufficient to overcome the ‘wrong’/hurtful pruning mask (panel F).
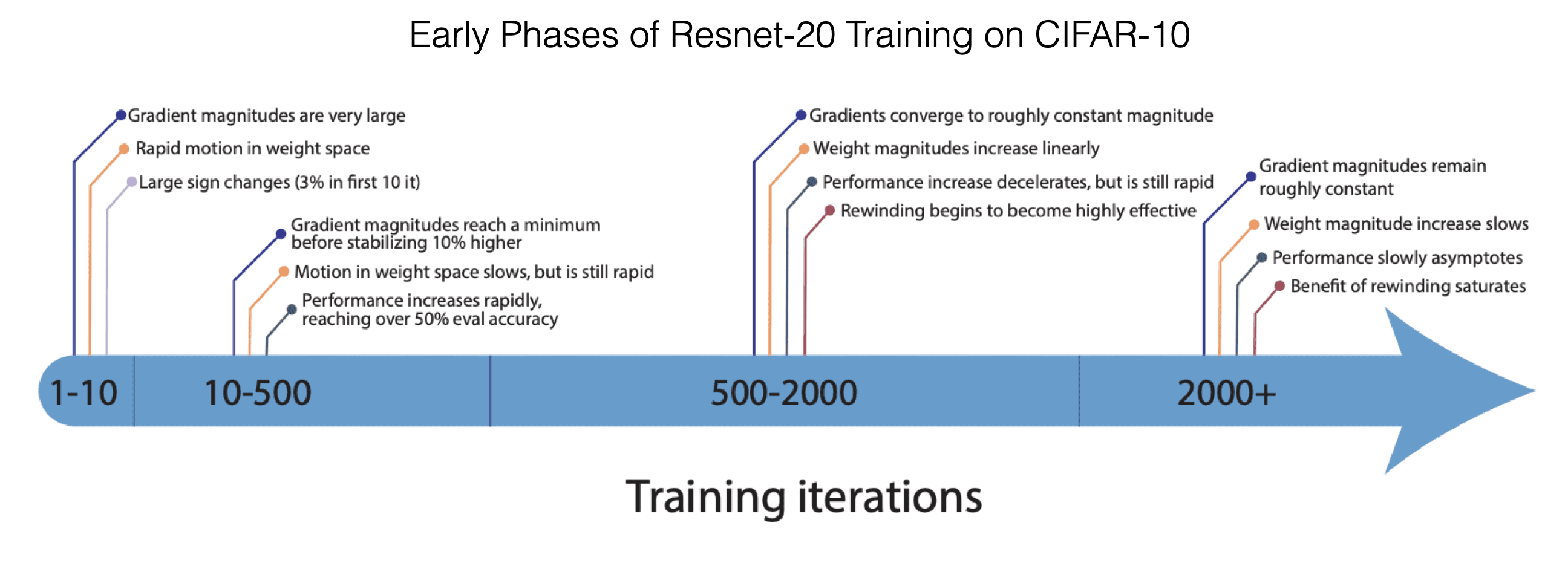
Fig. 9: Early Phase key results. Source: Adapted from Frankle et al. (2020b)
All in all, this provides evidence that it is very hard to overcome the necessity of using rewinding since the emergence of the matching initialization appears highly non-trivial. Self-supervised pre-training appears to provide a potential way to circumvent rewinding. Further insights in the early learning dynamics in training Resnet-20 on CIFAR-10 are summarized in the following awesome visualization by Frankle et al. (2020b):
Fig. 10: The Early Phase of NN Training. Source: Frankle et al. (2020b)
Detecting Winning Tickets with Little to No Training 
While the original work by Jonathan Frankle provides an empirical existence proof, finding tickets is tricky and costly. IMP requires repeated training of sparser and sparser networks, something not every PhD researcher can do (without being hated by their lab members ![]() ). The natural next question becomes how one can identify such networks with less compute. Here are two recent approaches which attempt to do so:
). The natural next question becomes how one can identify such networks with less compute. Here are two recent approaches which attempt to do so:
You, Li, Xu, Fu, Wang, Chen, Lin, Wang, & Baraniuk (2020) - Drawing Early-Bird Tickets: Towards more efficient training of deep networks
Paper | Code
You, Li, Xu, Fu, Wang, Chen, Lin, Wang, & Baraniuk (2020) identify winning tickets early on in training (hence ‘early-bird’ tickets) using a low cost training scheme which combines early stopping, low precision and large learning rates. They argue that this is due to the two-phase nature of optimization trajectories of neural networks (Saxe et al., 2013; Rahaman et al., 2018):
- A robust first phase of learning lower frequency/large singular value components.
- An absorbing phase of learning higher frequency/low singular value components.
By focusing on only identifying a connectivity pattern it is possible to identify early-bird tickets already during phase 1. A major difference to standard LTH work is that You et al. (2020) prune entire convolution channels based on their batch normalization scaling factor. Furthermore, pruning is performed iteratively within a single training run.
The authors empirically observe that the pruning masks change significantly during the first epochs of training but appear to converge soon (see left part of the figure below).
Fig. 14: Mask Convergence & Early Bird Algorithm. Source: Adapted from You et al. (2020)
Hence, they conclude that hypothesis of early emergence is true and formulate a suited detection algorithm: To detect the early emergence they propose a mask distance metric that computes the Hamming distance between two pruning masks at two consecutive pruning iterations. If the distance is smaller than a threshold $\epsilon$, they stop to prune. The resulting early-bird ticket can then simply be retrained to restore performance.
Tanaka, Kunin, Yamins, & Ganguli (2020) - Pruning neural networks without any data by iteratively conserving synaptic flow
Paper | Code
While You et al. (2020) asked whether it is possible to reduce the amount of required computation, they still need to train the model on the data. Tanaka et al. (2020), on the other hand, answer a more ambitious question: Can we obtain winning tickets without any training and in the absence of any data? They argue that the biggest challenge to pruning at initialisation is the problem of layer collapse - the over-eagerly pruning of an entire layer which renders the architecture untrainable (since the gradient flow is cut-off).
Think of an MLP that stacks a set of fully-connected layers. Layer collapse can be avoided by keeping a single weight per layer which corresponds to the theoretically achievable maximal compression. The level of compression which can be achieved by a pruning algorithm without collapse is called the critical compression. Ideally, we would like these two to be equal. Taking inspiration from flow networks, Tanaka et al. (2020) define a gradient-based score called synaptic saliency:
\[S(\theta) = \frac{\partial \mathcal{R}}{\partial \theta} \circ \theta\]where $\mathcal{R}$, $\theta$ and $\circ$ refer to a flow objective, the parameters and the Hadamard product, respectively. This metric is somewhat related to layerwise relevance propagation and measures a form of contribution. The paper then proves two conservation laws of saliency on a “micro”-neuron and “macro”-network level. This allows the authors to show that - for sufficient compression - gradient-based methods will prune large layers entirely (if evaluated once). So why don’t we run into layer collapse in the IMP setting with training? Tanaka et al. (2020) show that this is due to gradient descent encouraging layer-wise conservation as well as iterative pruning at small rates. So any global pruning algorithm that wants to a maximal critical compression has to respect two things: positively score layer-wise conservation and iteratively re-evaluate the scores after pruning.
Fig. 15: Performance & Synaptic Flow Algorithm. Source: Adapted from Tanaka et al. (2020)
Based on these observations the authors define an iterative procedure which generates a mask that preserves the flow of synaptic strengths through the initialized network (see above). Most importantly this procedure is entirely data-agnostic and only requires a random initialization. They are able to outperform other ‘pruning at init’ baselines on CIFAR-10/100 and Tiny ImageNet. I really enjoyed reading this paper since it exploits a theoretical result by turning it into an actionable algorithm.
Do Tickets Generalize across Datasets, Optimizers and Domains? 


Morcos, Yu, Paganini & Tian (2019) - One ticket to win them all: Generalizing lottery ticket initializations across datasets and optimizers
Paper | Code
A key question is whether matching tickets overfit. What does overfitting mean in the context of subnet initialization? The ticket is generated on a specific dataset (e.g. MNIST, CIFAR-10/0, ImageNet), with a specific optimizer (SGD, Adam, RMSprop), for a specific domain (vision) and a specific task (object classification). It is not obvious if a ticket would still be a winner if we would change any one of these ingredients. But what we are really interested in is to find the right inductive biases for learning - in a general sense.
Therefore, Morcos, Yu, Paganini & Tian (2019) asked whether one could identify a matching ticket on one vision dataset (e.g. ImageNet) and transfer it to another (e.g. CIFAR-100). The key question being whether the lottery ticket effect would hold up after training the matching ticket on the new dataset. The procedure goes as follows:
- Find a lottery ticket on a source dataset using IMP.
- Evaluate the source lottery ticket on a new target dataset by training it until convergence.
So at this point you might ask yourself how do input/output shape work in this case? At least I did ![]() . Since we operate on images and the first layer in the of considered networks case is a convolution, we don’t have to change anything about the first hidden layer transformation. Puh. At the stage of network processing where we transition from convolution to fully-connected (FC) layers, Morcos et al. (2019) use global average pooling in order to make sure that regardless of the channel size (which is going to differ between datasets) the FC layer dimensions work out. Last but not least, the final layer has to be excluded from the lottery ticket transfer and is instead randomly initialized. This is because different datasets have different numbers of target classes. This procedure is different from traditional transfer learning since we do not transfer representations (in the form of trained weights) but an initialization and mask found on a separate dataset. So what do Morcos et al. (2019) find?
. Since we operate on images and the first layer in the of considered networks case is a convolution, we don’t have to change anything about the first hidden layer transformation. Puh. At the stage of network processing where we transition from convolution to fully-connected (FC) layers, Morcos et al. (2019) use global average pooling in order to make sure that regardless of the channel size (which is going to differ between datasets) the FC layer dimensions work out. Last but not least, the final layer has to be excluded from the lottery ticket transfer and is instead randomly initialized. This is because different datasets have different numbers of target classes. This procedure is different from traditional transfer learning since we do not transfer representations (in the form of trained weights) but an initialization and mask found on a separate dataset. So what do Morcos et al. (2019) find?
-
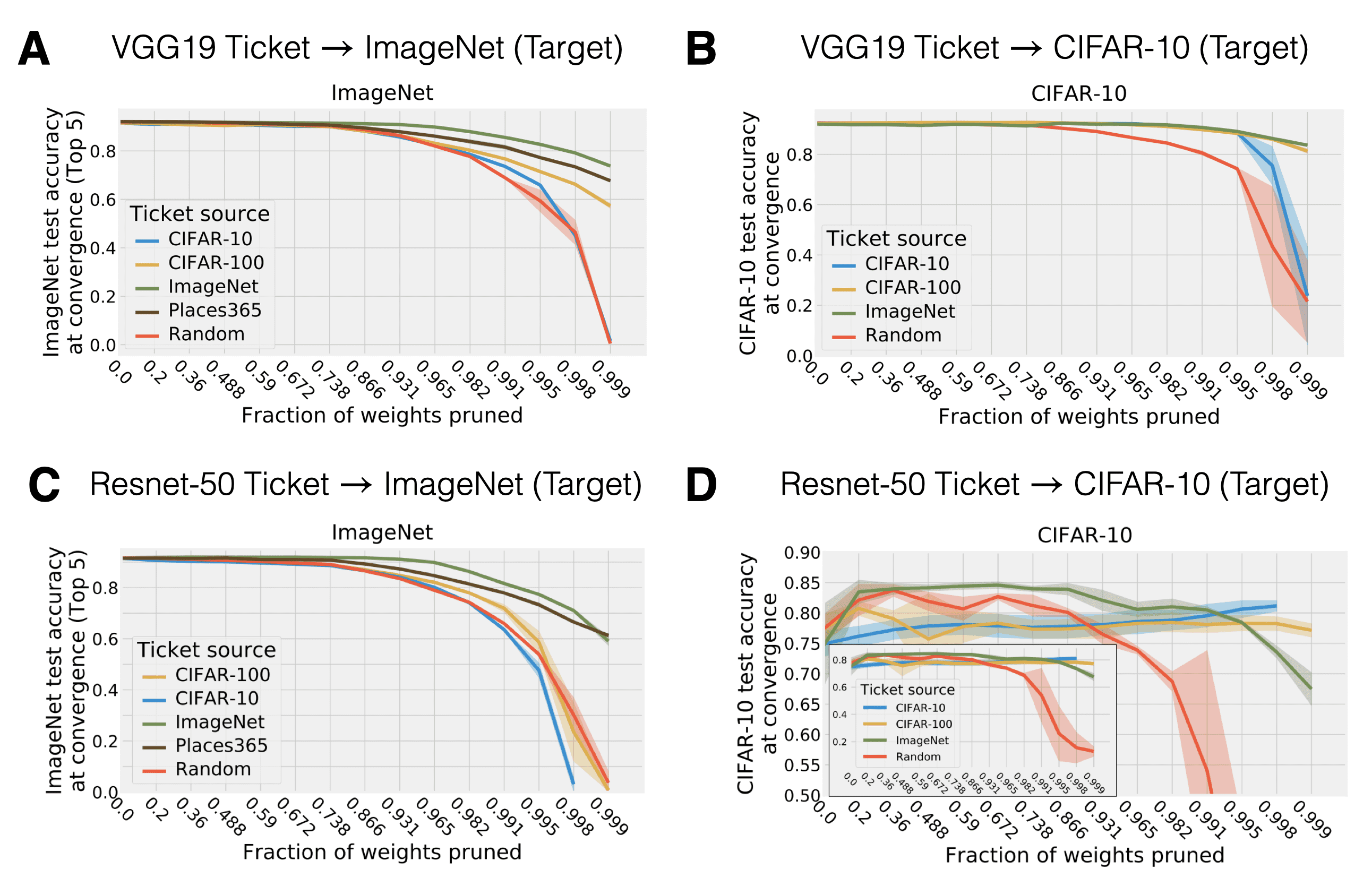
Panel A and Panel B: Transferring VGG-19 tickets from a small source dataset to ImageNet performs well - but worse than a ticket that is directly inferred on the target dataset. Tickets inferred from a larger dataset than the target dataset, on the other hand, perform even better than the ones inferred from the target dataset.
-
Panel C and Panel D: Approximately the same holds for Resnet-50. But one can also observe that performance degrades already for smaller pruning fractions than Resnet-50 (sharper “pruning” cliff for Resnet-50 than VGG-19).
Fig. 11: Transfer of tickets across datasets. Source: Adapted from Morcos et al. (2019)
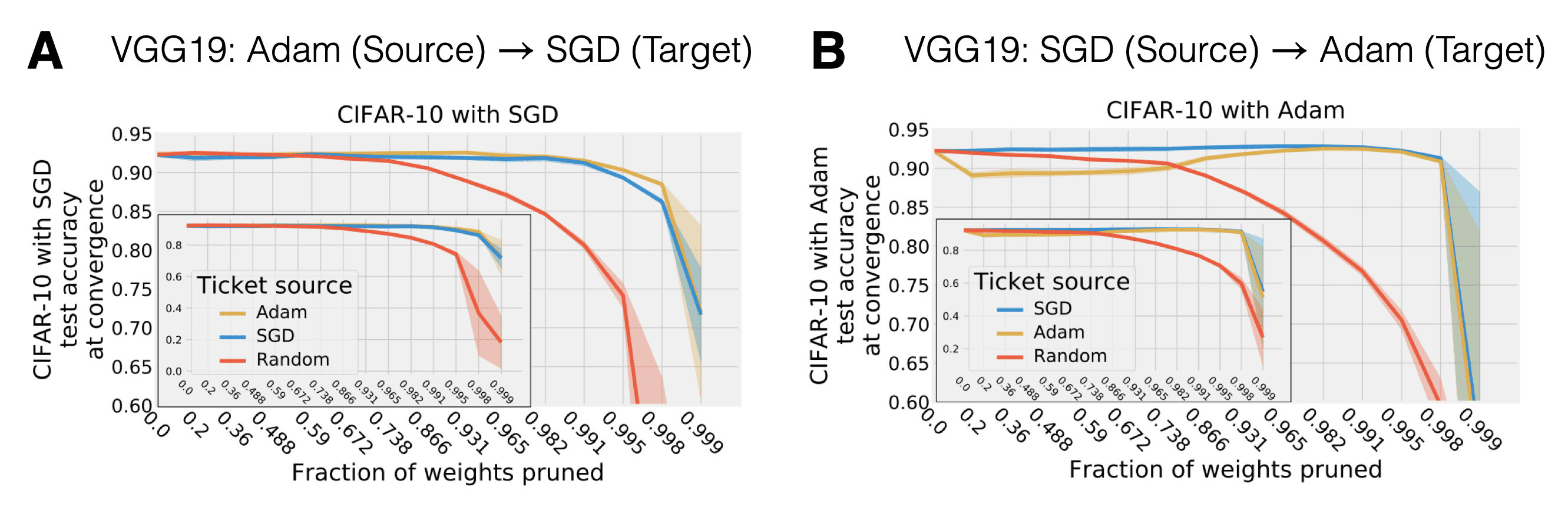
Finally, Morcos et al. (2019) also investigated whether a ticket inferred with one optimizer transfers to another. And yes, this is possible for VGG-19 if one carefully tunes learning rates. Again this is indicative that lottery tickets encode inductive biases that are invariant across data and optimization procedure.
Fig. 12: Transfer of tickets across optimizers. Source: Adapted from Morcos et al. (2019)
So what? This highlights a huge potential for tickets as general inductive bias. One could imagine finding a robust matching ticket on a very large dataset (using lots of compute). This universal ticket can then flexibly act as an initializer for (potentially all/most) loosely domain-associated tasks. Tickets, thereby, could - similarly to the concept of meta-learning a weight initialisation - perform a form of amortized search in weight initialization space.
Yu, Edunov, Tian, & Morcos (2019) - Playing the lottery with rewards and multiple languages: lottery tickets in RL and NLP
Paper
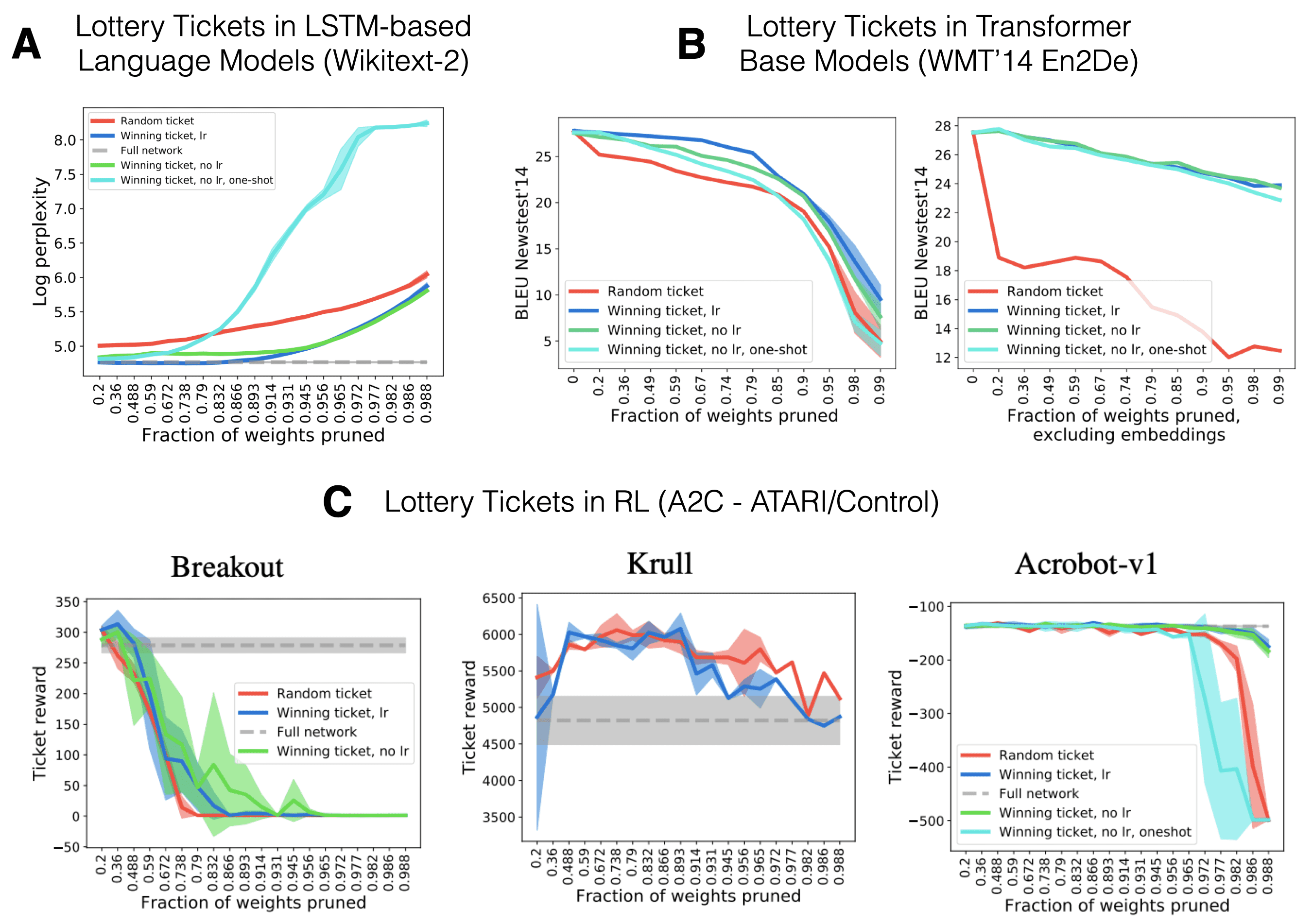
Until now we have looked at subnetwork initialisations in the context computer vision tasks. How about different domains with non-cross-entropy-based loss functions? (Yu, Edunov, Tian, & Morcos, 2019) investigate the extension to language models (LSTM-based and Transformer models) as well as the Reinforcement Learning (actor-critic methods) setting. There are several differences to the previous work in vision: First, we also prune other types of layers aside from convolutional filters and FC layers (recurrent & embedding layers and attention modules). Second, we train on very different loss surfaces (e.g. a non-stationary actor-critic loss). And finally, RL networks usually have a lot less parameters than large vision networks (especially for continuous control) which potentially makes it harder to prune at high levels of sparsity.
Fig. 13: Tickets in Language Models & RL. Source: Adapted from Yu et al. (2019)
In short - yes, there exit sparse initializations which significantly outperform random subnetworks for both language as well as RL tasks. Most interestingly, the authors find that one is able to prune up to 2/3 of all transformer weights while still obtaining strong performance. Late rewinding and iterative pruning are again key and embedding layers seem to be very overparametrized. Therefore, they are mainly targeted by IMP. For RL, on the other hand, well-performing pruning levels strongly varied across all considered games. This indicates that for some tasks standard CNN-based actor-critic networks have way too many parameters. This is most likely a function of RL benchmarks consisting of many games which are all being learned by the same architecture setup.
Open Research Questions 
The lottery ticket hypothesis opens up many different views on topics such as optimization, initialisation, expressivity vs. trainability and the role of sparsity/over-parametrization. At the current point in time there are way more unanswered than answered questions - and that is what excites me! Here are a few of the top of my head:
-
What are efficient initialisation schemes that evoke lottery tickets? Can meta-learning yield such winning ticket initialisation schemes (in compute wonderland)? Is it possible to formalise optimisation algorithms that exploit lottery tickets? Can the effects of connectivity and weight initialisation be disentangled? Can winning tickets be regarded as inductive biases?
-
A network that has been initialized with weights that were pretrained on only half of the training data, the final network (trained on the full dataset) always yields a generalization gap (Ash & Adams, 2019). In other words - pretraining on a subset of the data generalizes worse than training from a random initialisation. Can lottery tickets overcome this warm starting problem? This should be an easy extension to investigate following Morcos et al. (2019).
-
In which way do lottery tickets differ between domains (vision, language, RL) and tasks (classification, regression, etc.)? Are the differences a function of the loss surface and can we extract regularities simply from the masks?
All in all there is still a lot to discover and many lotteries to be won ![]() .
.
Some Final Pointers & Acknowledgements
I would like to thank Jonathan Frankle for valuable feedback, pointers & the open-sourcing of the entire LTH code base (see the open_lth repository). Furthermore, a big shout out goes to Joram Keijser and Florin Gogianu who made this blogpost readable
If you still can’t get enough of the LTH, these pointers are worth checking out:
- Jonathan Frankle’s ICLR Best Paper Award Talk - great 10 minute introduction of the key ideas and results with very digestible slides!
- Ari Morcos’ RE-WORK talk on generalising tickets across datasets.
- Jonathan Frankle’s contribution to the NeurIPS 2019 retrospectives in ML workshop & the accompanying personal story (beginning at 12:30 minutes)
- I recommend everyone to have a look at the evolution of the original paper and the different versions of the ArXiv preprint. Especially for a researcher at the beginning of their path, it was really enlightening to see the trajectory and scaling based on more and more powerful hypothesis testing.
- If you are interested in some maths and have an affinity for concentration inequalities, check out Malach et al. (2020). They formally prove the LTH as well as posit an even stronger conjecture: Given a large enough dense network there exists an subnetwork that achieves matching performance without any additional training.
- Checkout this GitHub repository with tons of recent (and not so recent) pruning papers.
You can find a pdf version of this blog post here. If you use this blog in your scientific work, please cite it as:
@article{lange2020_lottery_ticket_hypothesis,
title = "The Lottery Ticket Hypothesis: A Survey",
author = "Lange, Robert Tjarko",
journal = "https://roberttlange.github.io/year-archive/posts/2020/06/lottery-ticket-hypothesis/",
year = "2020",
url = "https://roberttlange.github.io/posts/2020/06/lottery-ticket-hypothesis/"
}
References 
- Ash, J. T., and R. P. Adams. (2019): “On the Difficulty of Warm-Starting Neural Network Training,” arXiv preprint arXiv:1910.08475, .
- Frankle, J., and M. Carbin. (2019): “The lottery ticket hypothesis: Finding sparse, trainable neural networks,” arXiv preprint arXiv:1803.03635, .
- Frankle, J., G. K. Dziugaite, D. M. Roy, and M. Carbin. (2019): “Stabilizing the lottery ticket hypothesis,” arXiv preprint arXiv:1903.01611, .
- Frankle, J., D. J. Schwab, and A. S. Morcos. (2020): “The Early Phase of Neural Network Training,” arXiv preprint arXiv:2002.10365, .
- Frankle, J., G. K. Dziugaite, D. M. Roy, and M. Carbin. (2020): “Linear Mode Connectivity and the Lottery Ticket Hypothesis,” arXiv preprint arXiv:1912.05671, .
- Gale, T., E. Elsen, and S. Hooker. (2019): “The state of sparsity in deep neural networks,” arXiv preprint arXiv:1902.09574, .
- Gaier, A., and D. Ha. (2019): “Weight Agnostic Neural Networks,” Advances in Neural Information Processing Systems, .
- Liu, Z., M. Sun, T. Zhou, G. Huang, and T. Darrell. (2018): “Rethinking the value of network pruning,” arXiv preprint arXiv:1810.05270, .
- Malach, E., G. Yehudai, S. Shalev-Shwartz, and O. Shamir. (2020): “Proving the Lottery Ticket Hypothesis: Pruning is All You Need,” arXiv preprint arXiv:2002.00585, .
- Morcos, A., H. Yu, M. Paganini, and Y. Tian. (2019): “One Ticket to Win Them All: Generalizing Lottery Ticket Initializations across Datasets and Optimizers,” Advances in Neural Information Processing Systems, .
- Rahaman, N., A. Baratin, D. Arpit, F. Draxler, M. Lin, F. A. Hamprecht, Y. Bengio, and A. Courville. (2018): “On the spectral bias of neural networks,” arXiv preprint arXiv:1806.08734, .
- Renda, A., J. Frankle, and M. Carbin. (2020): “Comparing rewinding and fine-tuning in neural network pruning,” arXiv preprint arXiv:2003.02389, .
- Saxe, A. M., J. L. McClelland, and S. Ganguli. (2013): “Exact solutions to the nonlinear dynamics of learning in deep linear neural networks,” arXiv preprint arXiv:1312.6120, .
- Tanaka, H., D. Kunin, D. L. K. Yamins, and S. Ganguli. (2020): “Pruning neural networks without any data by iteratively conserving synaptic flow,” arXiv preprint arXiv:2006.05467, .
- You, H., C. Li, P. Xu, Y. Fu, Y. Wang, X. Chen, Y. Lin, Z. Wang, and R. G. Baraniuk. (2020): “Drawing early-bird tickets: Towards more efficient training of deep networks,” arXiv preprint arXiv:1909.11957, .
- Yu, H., S. Edunov, Y. Tian, and A. S. Morcos. (2019): “Playing the lottery with rewards and multiple languages: lottery tickets in RL and NLP,” arXiv preprint arXiv:1906.02768, .
- Zhou, H., J. Lan, R. Liu, and J. Yosinski. (2019): “Deconstructing Lottery Tickets: Zeros, Signs, and the Supermask,” Advances in Neural Information Processing Systems, .